Equivalent Circuit of Transformer
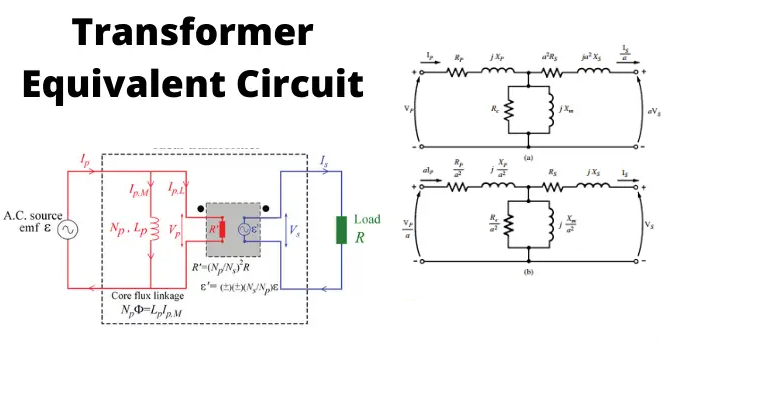
The equivalent circuit diagram of a transformer is a simplified circuit in which the impedance, resistance, and leakage reactance of the transformer can be more easily calculated.
The equivalent impedance of the transformer is an important parameter to be calculated. This calculation requires the equivalent circuit of the transformer referred to as the primary or equivalent circuit of the transformer referred to secondary sides respectively. Percentage impedance is also a very essential parameter of the transformer.
Special attention is to be given to this parameter during installing a transformer in an existing electrical power system. The percentage impedance of different power transformers should be properly matched during the parallel operation of power transformers.
The percentage impedance can be derived from the equivalent impedance of the transformer so, it can be said that the equivalent circuit of the transformer is also required during the calculation of the % impedance.
Table of contents
1. Approximate Equivalent Circuit of Transformer
2. Equivalent Circuit of Transformer Referred to Secondary
3. Equivalent Circuit of Transformer Referred to Primary
Approximate Equivalent Circuit of Transformer
Since Io is very small compared to I1, it is less than 5% of full load primary current, Io changes the voltage drop insignificantly.
Hence, it is a good approximation to ignore the excitation circuit in the approximate equivalent circuit of the transformer.
The winding resistance and reactance being in series can now be combined into equivalent resistance and reactance of the transformer, referred to any particular side. In this case, it is side 1 or the primary side.


Equivalent Circuit of Transformer Referred to Secondary
In a similar way, the approximate equivalent circuit of the transformer referred to as secondary can be drawn.
Where the equivalent impedance of the transformer referred to as secondary, can be derived as:


Equivalent Circuit of Transformer Referred to Primary
For drawing the equivalent circuit of the transformer referred to as primary, first, we have to establish a general equivalent circuit of the transformer then, we will modify it for referring from the primary side. To do this, first, we need to recall the complete vector diagram of a transformer shown in the figure below.

Let us consider the transformation ratio be,

In the figure above, the applied voltage to the primary is V1, and the voltage across the primary winding is E1. The total current supplied to the primary is I1. So the voltage V1 applied to the primary is partly dropped by I1Z1 or I1R1 + j.I1X1 before it appears across the primary winding.
The voltage that appeared across the winding is countered by primary induced emf E1. So voltage equation of this portion of the transformer can be written as,

The equivalent circuit for that equation can be drawn below,

From the vector diagram above, it is found that the total primary current I1 has two components, one is no–load component Io and the other is load component I2′. As this primary current has two components or branches, so there must be a parallel path with the primary winding of the transformer.
This parallel path of current is known as the excitation branch of an equivalent circuit of the transformer. The resistive and reactive branches of the excitation circuit can be represented as


The load component I2′ flows through the primary winding of the transformer and the induced voltage across the winding is E1 as shown in the figure right.
This induced voltage E1 transforms to secondary and it is E2 and the load component of primary current I2′ is transformed to secondary as secondary current I2. The current of the secondary is I2.
So the voltage E2 across secondary winding is partly dropped by I2Z2 or I2R2 + j.I2X2 before it appears across the load. The load voltage is V2.
The complete equivalent circuit of the transformer is shown below.

Now if we see the voltage drop in the secondary from the primary side, then it would be ′K′ times greater and would be written as K.Z2.I2.
Again I2′.N1 = I2.N2

Therefore,

From the above equation, the secondary impedance of the transformer referred to as primary is,

So, the complete equivalent circuit of the transformer referred to as primary is shown in the figure below:

Source: Electrical4u